Volt Drop Calculations for Power Limited Circuits

 

By Ed Lethert, "The Low Voltage Guy"

 

I have been intrigued with the subject of volt drop for more than 45 years. Can't say I know why that is ... I just am.

I've been teaching electrical exam prep classes and continuing education classes related to Minnesota's power limited technician license for several years now. The exam prep course includes a module on volt drop because there are volt drop problems on the exam. I also teach it in some continuing education classes as it applies to power-limited work, such as fire alarm systems, security systems, irrigation systems, etc.

I hope the reader has a basic understanding of volt drop and its effect on electrical circuits. We all know the copper wire is a good conductor of electricity. It is not a perfect conductor, however, and its use will introduce some loss in a typical circuit. This loss is caused by the resistance of the wire varies according to the circular mil area of the wire. A large diameter conductor has a large CMA and lower resistance. A small diameter wire has a smaller CMA and higher resistance. One can easily see this by turning to Table 8 of Chapter 9 of the NEC (Conductor Properties) and looking at the DC resistance values.

In the electrical industry, the formula for calculating volt drop is:

VD =	2 × K × L × I
	CM

VD = Conductor Volt Drop in Volts (both conductors)

K = Conductor DC Resistance in Circular Mil-Feet

(K = 12.6 Ohms for solid copper conductors at 75°C)

(K = 12.9 Ohms for stranded copper conductors at 75°C)

L = Circuit Length in Feet (one way)

I = Circuit Current in Amperes

CM = Conductor Cross-sectional Area in Circular Mils

(See NEC, Chapter 9, Table 8, page 635 (2005) or page 625 (2002))

This is the formula most often taught to electrical engineers and electricians.

A variation of the volt drop formula uses the DC resistance values from Table 8 of Chapter 9 of the NEC (Conductor Properties). This simplified formula eliminates the need to use circular mil area in the calculation or, for that matter, the need to understand it. It is the formula that is taught in the classes mentioned at the beginning of this article.

VD =	2 × DCR × L × I
	1000

VD = Conductor Volt Drop in Volts (both conductors)

DCR = Conductor DC Resistance in Ohms per 1000 Feet

(See NEC, Chapter 9, Table 8, page 635 (2005) or page 625 (2002))

L = Circuit Length in Feet (one way)

I = Circuit Current in Amperes

When used correctly, both formulas produce the same result.

Neither of the formulas we've look at considers the effect of the conductor resistance on the circuit. Simply stated, the resistance of the conductors increases the total circuit resistance by an amount equal to the conductor resistance. Assuming that the voltage of the power source is constant, it then follows that the total current in the circuit will decrease. A decrease in total current will result in a decrease in the volt drop of the conductors, thereby reducing the volt drop of the circuit. Note: The circuit behavior described in this paragraph does not apply to induction motors, or to any other equipment that produces back-EMF.

For example, let's take a look at a typical low voltage irrigation circuit. These circuits generally operate at 24 Volts AC. A modern valve solenoid draws about 0.25 Amps. The basic circuit, excluding any conductor resistance, can be determined by using Ohm's law. The solenoid has a resistance of 96 Ohms (24 Volts ÷ 0.25 Amps). Yes, I know … this is an AC circuit and the solenoid has impedance, not just resistance. We're going to keep it simple for now and assume that the solenoid has only resistance.

Next, let's assume that a circuit consists of 1500 feet of 18 gauge, 2 conductor, direct burial cable. The conductor temperature is assumed to be 20 degrees Centigrade.

The total resistance of the conductors is calculated to be 19.2 Ohms. A current of 0.25 Amps appears to produce a volt drop of 4.8 Volts. This is 20 percent volt drop in a circuit whose power source is 24 Volts. The irrigation industry suggests that the volt drop for irrigation valve solenoids not exceed 16-17 percent. Are we over the limit? It would seem so, but … .

The conductor resistance (19.2 Ohms) has increased the circuit's total resistance by an additional 19.2 Ohms. Instead of being just the 96 Ohms of the solenoid, it is actually 115.2 Ohms (96 Ohms + 19.2 Ohms). The current that was 0.25 Amps is now reduced to 0.21 Amps (24 Volts ÷ 115.2 Ohms). The volt drop of the conductors is more realistically 4.0 Volts (19.2 Ohms × 0.21 Amps). The percent of volt drop is only 16.7 percent (100 × 4 Volts ÷ 24 Volts).

Here's the bottom line. When using the formulas we've discussed, the volt drop calculation will result in a value that is greater than the actual volt drop. The error—believe it or not—is the same as the calculated percent of volt drop. In other words, if one calculates 5 percent volt drop, the actual volt drop is 4.76 percent (a five percent error). In the case of our irrigation circuit, the error is 20 percent because the basic volt drop was calculated to be 20 percent. The actual volt drop is 16.7 percent (20 ÷ 1.2 = 16.67 percent).

These errors only get worse as the percent of volt drop increases. Interestingly, when the simple volt drop is calculated to be 100 percent of the supply voltage, the actual volt drop is only 50 percent (100 ÷ (1 + 1.00) = 100 ÷ 2 = 50 percent volt drop). How's that for an error!?

It will be argued by many that a 5 percent error is not a concern when dealing with circuits of electric light and power, at least in most cases. Besides, because the error is "to the good." It does not cause faulty designs or installations.

BUT ... it can be a problem when dealing with volt drop for power-limited circuits that operate at lower voltages, especially those that run significant distances.

There is a simple correction formula that permits one to determine the more precise percent volt drop after first calculating the simple volt drop. The formula is:

Precise Percent Volt Drop = 100 × SVD ÷ (1 + SVD)

SVD = Simple Percent Volt Drop (expressed as a decimal, i.e. 20% is 0.20)

Example:

Precise Percent Volt Drop = 100 × 0.20 ÷ (1 + 0.20)

100 × 0.20 ÷ (1 + 0.20) = 16.7 Percent Volt Drop (Precise)

 

This formula can be further simplified to:

Precise Percent Volt Drop = Simple Percent Volt Drop ÷ (1 + SVD)

20 ÷ (1 + 0.20) = 16.7 Percent Volt Drop (Precise)

A table of these values demonstrates the result of this correction calculation.

The author has constructed a detailed spreadsheet that details these calculations and their effect on circuit performance.

Click here to download the excel spreadsheet.

Click here to download the information in pdf format.

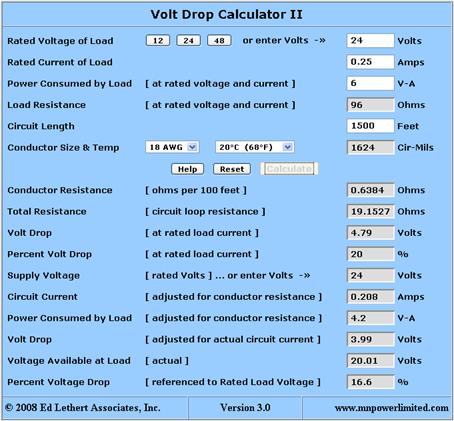Let's make this as easy as possible for everyone. The author has designed a volt drop calculator that can assist in determining the actual volt drop and percent volt drop for power-limited circuits.

The user first selects the rated voltage of the load, either by using the buttons provided or by entering a voltage of choice. Next they enter the load's current draw or power consumption. Finally, they enter the circuit length. Apologies to the SI unit aficionados, everything is in inch-pound (English) units (as it should be).

The calculator defaults to 18 gauge copper conductors and a conductor temperature of 20° C. Circuit length and conductor temperature can be easily adjusted to accommodate other values where needed.

The supply voltage (of the power source) defaults to the selected rated voltage but can be adjusted to account for other conditions. For example, HVAC control systems often use 27 to 28 Volts as the supply voltage for their 24-Volt relays and contactors. This must be taken into consideration where the condition exists.

I remind the reader once again that this calculator will not work with induction motor type loads, or with any other equipment that produces back-EMF. It does work with AC relays and AC solenoid type loads as they do not produce back-EMF.

The calculator is available at the author's web site at www.mnpowerlimited.com

 

Conductor Temperature

The conductor temperature is also a matter of concern for power-limited circuit designers and installers. Volt drop calculations must be based on real world conditions. One generally does not find the conductors of power-limited circuits operating at temperatures anywhere near 75° Centigrade. The DC resistance of 1000 feet of 18 gauge, solid copper wire is 6.384 Ohms at 20° C. At one amp the volt drop is 6.4 Volts. The resistance is 7.77 Ohms at 75° C (from Table 1, Chapter 9 of the NEC). At this temperature the same volt drop is 7.8 Volts. The resistance is only 6.148 Ohms at 10° C (50° F), the temperature of many direct buried, power-limited conductors.

Summary

Volt drop and percent volt drop are not likely to be a high priority design or installation concern for most residential and commercial structures where ampacity dominates. On the other hand, ampacity is seldom a concern for power-limited circuits. Volt drop becomes the dominant concern as system voltage decreases, as conductor size decreases, and as circuit length increases. The NEC reminds us in a fine print note at the beginning of Article 725 that "The circuits described herein are characterized by usage and electrical power limitations that differentiate them from electric light and power circuits; therefore, alternative requirements to those of Chapters 1 through 4 are given with regard to minimum wire sizes, derating factors, overcurrent protection, insulation requirements, and wiring methods and materials." This article is addressing primarily power-limited circuits and clearly states that they are different from circuits of electric light and power. They must be given the required attention.

 

Ed Lethert is an electrical instructor and technical consultant in Minneapolis, Minnesota. He can be contacted at 763-545-0030 or Ed@mnpowerlimited.com.  His web site is www.mnpowerlimited.com.